마름모 넓이 공식 완벽 가이드: 유도부터 실전 예시까지
수학 교과서에서 마름모(평행사변형의 특수한 경우로, 네 변의 길이가 모두 같은 사각형)는 자주 등장하지만, 넓이 공식을 정확히 유도해 본 경험은 의외로 적습니다.
본 글에서는 마름모 넓이 구하는 공식을 다양한 관점(높이, 대각선, 좌표 기하, 벡터)으로 증명하고, 실전 예시·응용까지 총망라합니다. 특히 수능·내신·각종 공학 시험 등에서 출제되는 마름모 넓이 공식 관련 기출 유형을 분석해, 실수 포인트와 풀이 전략을 함께 제시합니다.
마름모의 정의와 기본 성질
네 변의 길이가 모두 같은 사각형
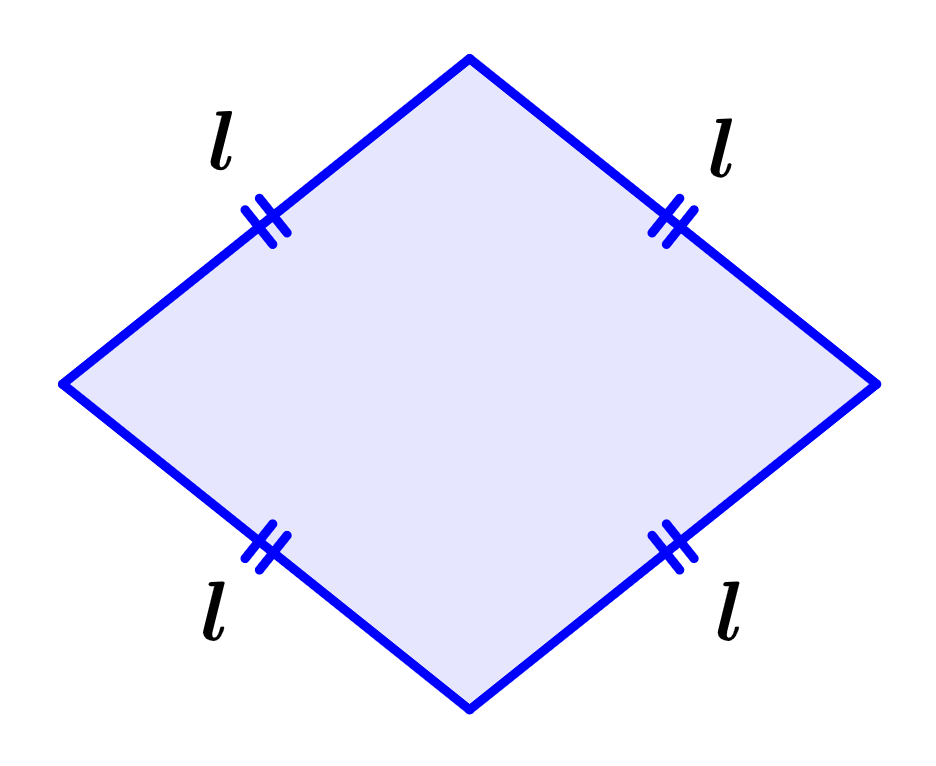
- 네 변이 모두 같은 길이를 갖는 볼록 사각형.
- 두 쌍의 대각선이 서로 수직으로 교차하며, 교차점은 서로를 이등분.
- 평행사변형의 모든 성질(대변 평행, 대각선 교차점에서 양쪽이 같음)을 그대로 갖는다.
필수 용어 정리
- 한 변의 길이($a$)
- 높이($h$): 한 변에 내린 수선의 길이
- 대각선 길이($d_1, d_2$)
마름모 넓이 구하는 공식 유도

높이 이용: $S = a \times h$

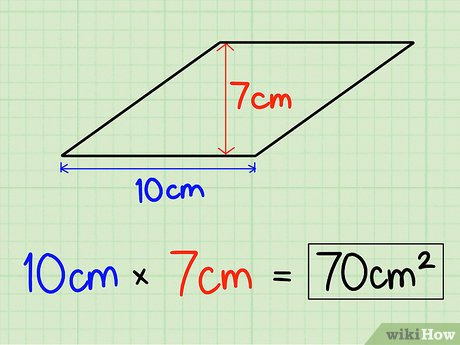
마름모 넓이 구하는 공식 유도 과정
- 마름모를 한 변 $a$, 높이 $h$로 본다.
- 밑변이 $a$, 높이가 $h$인 평행사변형 넓이 공식을 그대로 적용.
- $S = a \times h$.
특이점
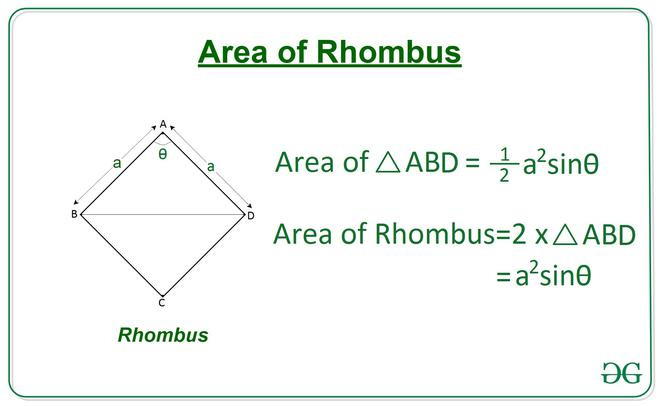
- 변과 변 사이 각 $\theta$를 안다면 $h = a\sin\theta$ ⇒ $S = a^2 \sin\theta$.
대각선 이용 마름모 넓이 구하는 공식: $S = \dfrac{d_1 d_2}{2}$

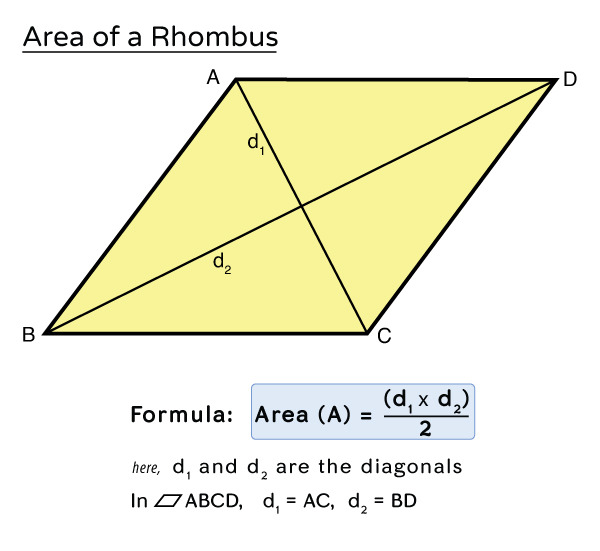
유도 과정
- 대각선들이 수직으로 교차하므로, 사각형을 네 개의 합동 직각삼각형으로 분해 가능.
- 직각삼각형 넓이 합이 $\dfrac{d_1 d_2}{2}$.
주의점
- 대각선이 수직 교차한다는 성질은 마름모이기에 항상 성립.
- 일반 평행사변형에는 적용 불가.
좌표 기하적 증명
- 좌표평면에 마름모 중심을 원점, 대각선들을 $x$축과 $y$축 상에 배치.
- 꼭짓점은 $(\frac{d_1}{2},0),(0,\frac{d_2}{2}),(-\frac{d_1}{2},0),(0,-\frac{d_2}{2})$.
- 슈호핑(뱀꼬리) 공식 또는 다각형 넓이 공식으로 계산 ⇒ $\frac{d_1 d_2}{2}$.
벡터 내적 이용
- 인접 변 벡터 $\mathbf{u}, \mathbf{v}$는 $|\mathbf{u}| = |\mathbf{v}| = a$, 끼인각 $\theta$.
- 넓이 $S = |\mathbf{u} \times \mathbf{v}| = |\mathbf{u}|,|\mathbf{v}|,\sin\theta = a^2 \sin\theta$.
- 대각선 벡터 $\mathbf{d_1} = \mathbf{u}+\mathbf{v},\ \mathbf{d_2} = \mathbf{u}-\mathbf{v}$.
- $|\mathbf{d_1}|\ |\mathbf{d_2}|\sin90^\circ = 2|\mathbf{u}|\ |\mathbf{v}|\sin\theta = 2a^2\sin\theta$ ⇒ $S = \dfrac{d_1 d_2}{2}$.
실전 예시
예시 1: 기본 숫자 대입
- 변 $a = 10\text{ cm}$, 높이 $h = 6\text{ cm}$.
- $S = 10 \times 6 = 60\text{ cm}^2$.
예시 2: 대각선 길이로 계산
- $d_1 = 12\text{ cm}, d_2 = 16\text{ cm}$.
- $S = \dfrac{12 \times 16}{2} = 96\text{ cm}^2$.
예시 3: 각도 이용
- 변 길이 $a = 5\text{ m}$, 끼인각 $\theta = 30^\circ$.
- $S = a^2 \sin\theta = 25 \times 0.5 = 12.5\text{ m}^2$.
예시 4: 실생활 활용(태양광 패널 설계)
- 마름모 형태 패널: 대각선 1.2 m, 1.8 m.
- 설치 면적 $S = \dfrac{1.2 \times 1.8}{2} = 1.08\text{ m}^2$.
- 패널 25장을 설치하면 총 $27\text{ m}^2$의 지면 확보 필요.
흔히 하는 실수 및 주의사항
대각선이 수직인지 확인 불량
- 정사각형·마름모에서는 항상 수직, 다른 사각형은 아님.
단위 미처 변환하지 않음
- 대각선 하나 cm, 다른 하나 mm라면 넓이 계산 전에 통일 필수.
높이와 대각선 헷갈림
- 높이는 변에 수직, 대각선은 꼭짓점 연결. 명확히 구분.
실생활 적용 사례
건축·인테리어
- 전통 한옥 창호 격자, 납작 마름모 문양 → 재료 소요 계산 시 넓이 공식 활용.
그래픽 디자인
- 로고·패턴 제작 시 동일 넓이 마름모 반복 배열 → 공백 최소화.
토목·측량
- 사선 도로 교차 구간(마름모형 안전지대) 도색 면적 산출.
연습 문제
문제 1
- 변 $a = 13\text{ cm}$, 끼인각 $\theta = 45^\circ$. 넓이는?
문제 2
- 대각선 길이가 각각 $18\text{ m}, 24\text{ m}$인 마름모. 사방 도랑(폭 1 m)을 두르면, 도랑의 넓이는?
문제 3
- 좌표 $A(0,5), B(4,3)$가 인접 변 끝. 마름모 넓이는?
해설
문제 1 해설
- $S = a^2 \sin\theta = 169 \times \frac{\sqrt{2}}{2} \approx 119.5\text{ cm}^2$.
문제 2 해설
- 마름모 넓이 $\frac{18 \times 24}{2} = 216\text{ m}^2$.
- 바깥으로 1 m 폭 확장하면 대각선 각각 2 m 증가 ⇒ $d'_1 = 20, d'_2 = 26$.
- 확장 후 넓이 $\frac{20 \times 26}{2} = 260\text{ m}^2$.
- 도랑 넓이 $260 - 216 = 44\text{ m}^2$.
문제 3 해설
- 두 벡터 $\mathbf{u} = (0,5),\ \mathbf{v} = (4,3)$.
- $|\mathbf{u}| = 5,\ |\mathbf{v}| = 5$ ⇒ 마름모 조건 충족.
- $\sin\theta = \dfrac{|\mathbf{u} \times \mathbf{v}|}{|\mathbf{u}||\mathbf{v}|} = \dfrac{|0\cdot3-5\cdot4|}{25} = \dfrac{20}{25} = 0.8$.
- $S = 5^2 \times 0.8 = 20$.
결론
- 마름모 넓이 공식은 두 형태(높이 이용, 대각선 이용)가 실전에서 모두 유용합니다.
- 대입 전 단위·조건을 반드시 확인하면 실수 예방 가능.
- 다양한 증명법을 이해하면, 낯선 문제에서도 응용력이 높아집니다.
- 본 포스트의 연습 문제·해설로 개념을 복습하고, 실생활 사례로 학습 동기를 확장해 보세요.
'수학 과학 공학' 카테고리의 다른 글
| 2026 수능 응시원서 접수 주의사항 및 준비물 (0) | 2025.08.29 |
|---|---|
| 2026학년도 대학입시 일정 2026 대입 전형 (0) | 2025.08.05 |
| 이등변 삼각형 넓이 공식 유도, 예시 (0) | 2025.07.22 |
| 등차수열의 합 공식 유도부터 실전 예시까지 (0) | 2025.07.20 |
| 사다리꼴 넓이 구하는 공식 유도, 예시 (0) | 2025.07.18 |



