이등변 삼각형 넓이 공식 유도, 예시
이 글에서는 이등변 삼각형의 넓이 공식을 여러 관점에서 유도하고, 다양한 예시를 통해 실제 계산 방법을 상세히 살펴봅니다. 이등변 삼각형은 두 변의 길이가 같은 특별한 삼각형으로, 기하학적 성질이 단순하면서도 응용 범위가 넓어 수학·공학·디자인 등 여러 분야에서 자주 활용됩니다.


본 포스팅은 이등변 삼각형 넓이 유도 과정을 단계별로 이해하기 쉽게 설명하고, 대표적인 예제 풀이를 통해 실전 감각을 기르는 데 초점을 맞췄습니다.
이등변 삼각형 넓이 공식 유도
이등변 삼각형의 정의
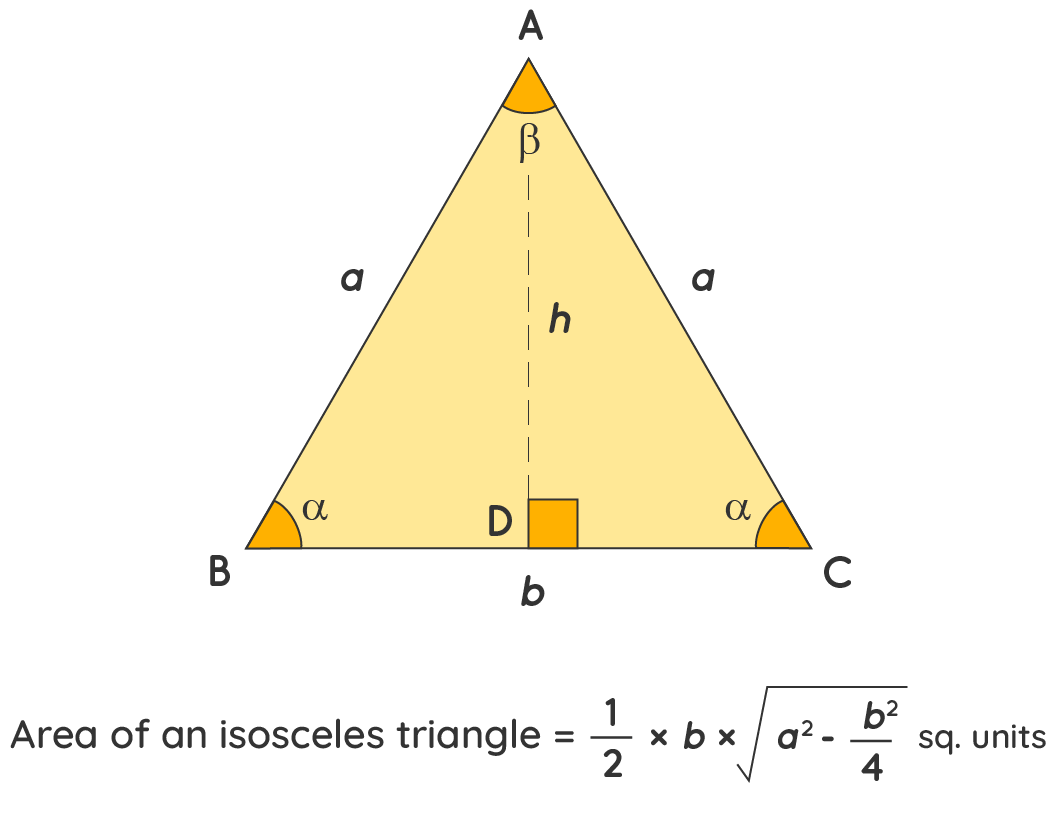
- 이등변 삼각형은 두 변의 길이가 같고, 나머지 한 변(밑변)의 길이가 다릅니다.
- 보통 밑변을 $b$, 양쪽 변(각변)을 $a$라고 표기합니다.
- 꼭짓점에서 밑변에 내린 수선의 길이를 ‘높이’ $h$라고 합니다.
기본 넓이 공식 적용
삼각형 전체의 넓이는 일반적으로 밑변과 높이를 이용해 구합니다.
$$
\text{넓이} = \frac{1}{2} \times \text{밑변} \times \text{높이}
$$
따라서 이등변 삼각형 역시,
$$
A = \frac{1}{2} , b , h
$$
로 표현할 수 있습니다.
높이 $h$의 도출
이제 $h$를 이등변 삼각형의 변 $a$, 밑변 $b$로 나타내 보겠습니다.
- 꼭짓점에서 밑변에 내린 수선은 밑변을 정확히 반으로 나눕니다.
- 밑변을 이등분하므로, 반쪽 길이는 $\tfrac{b}{2}$.
- 삼각형 $A$–$D$–$B$에서 직각삼각형을 이루므로, 피타고라스 정리를 적용합니다.
- $$
a^2 = h^2 + \Bigl(\tfrac{b}{2}\Bigr)^2
$$ - 이를 $h$에 대해 풀면
- $$
h = \sqrt{a^2 - \Bigl(\tfrac{b}{2}\Bigr)^2}
= \sqrt{a^2 - \frac{b^2}{4}}
$$
최종 넓이 공식
위 식을 넓이 공식에 대입하면
$$
A = \frac{1}{2} , b \times \sqrt{a^2 - \frac{b^2}{4}}
= \frac{b}{2} ,\sqrt{a^2 - \frac{b^2}{4}}
$$
또는
$$
A = \frac{b}{4} ,\sqrt{4a^2 - b^2}
$$
와 같은 형태로도 쓸 수 있습니다.
적용 예시
예시 1: 밑변과 각변으로 면적 구하기
- 조건: 이등변 삼각형의 각변 $a = 10$, 밑변 $b = 12$
- 높이 계산:
- $$
h = \sqrt{10^2 - \Bigl(\frac{12}{2}\Bigr)^2}
= \sqrt{100 - 36}
= \sqrt{64}
= 8
$$ - 넓이 계산:
- $$
A = \frac{1}{2} \times 12 \times 8 = 48
$$
예시 2: 헤론 공식을 활용한 면적
- 조건: 이등변 삼각형 $a = 13$, $b = 10$
- 준비: 반둘레 $s = \tfrac{a + a + b}{2} = \tfrac{13 + 13 + 10}{2} = 18$
- 헤론 공식:
- $$
A = \sqrt{s(s-a)(s-a)(s-b)}
= \sqrt{18 \times (18-13) \times (18-13) \times (18-10)}
= \sqrt{18 \times 5 \times 5 \times 8}
= \sqrt{18 \times 200}
= \sqrt{3600}
= 60
$$ - 피타고라스 검산:따라서
- $$
A = \frac{1}{2} \times 10 \times 12 = 60
$$ - $$
h = \sqrt{13^2 - \bigl(\tfrac{10}{2}\bigr)^2}
= \sqrt{169 - 25}
= \sqrt{144}
= 12
$$
로 일치합니다.
예시 3: 각도와 두 변으로 면적 구하기
- 조건: 이등변 삼각형의 각변 $a = 7$, 두 각변 사이의 각 $\theta = 50^\circ$
- 공식: 두 변 $a$, $a$ 사이의 각 $\theta$일 때
- $$
A = \frac{1}{2} a^2 \sin\theta
$$ - 계산:
- $$
A = \frac{1}{2} \times 7^2 \times \sin 50^\circ
= \frac{49}{2} \times 0.7660\ldots
\approx 18.767
$$
결론
이등변 삼각형의 넓이 공식은 ‘밑변×높이÷2’라는 기본 공식에 기초하여, 높이를 피타고라스 정리로 표현하거나 헤론 공식 및 삼각함수를 적용해 도출할 수 있습니다. 여러 방법을 이해하면 문제 상황에 맞춰 가장 효율적인 경로를 선택할 수 있으며, 각종 공학·디자인·건축 분야에서도 유연하게 활용할 수 있습니다. 특히 수학 시험에서는 주어진 정보(변, 높이, 각도 등)에 따라 적절한 공식을 선택하는 것이 관건입니다.



'수학 과학 공학' 카테고리의 다른 글
| 2026학년도 대학입시 일정 2026 대입 전형 (0) | 2025.08.05 |
|---|---|
| 마름모 넓이 구하는 공식 유도, 예시 (0) | 2025.07.26 |
| 등차수열의 합 공식 유도부터 실전 예시까지 (0) | 2025.07.20 |
| 사다리꼴 넓이 구하는 공식 유도, 예시 (0) | 2025.07.18 |
| 3호 태풍 문 경로 예상 (0) | 2025.07.02 |



